フィボナッチ数列は、数学の世界だけでなく、自然界やアートの領域にも深く根付いている不思議な数列です。この数列の魅力や特徴、発見者に関する情報を、今回のブログでご紹介します。数学に興味のある方も、そうでない方も、フィボナッチ数列の不思議な世界をご堪能ください。
1. フィボナッチ数列とは?
フィボナッチ数列は、数理的な興味に富んだ数の並びであり、自然数の特性を利用して構築されています。この数列の特徴は、その簡単な加算ルールにあります。最初の二つの項は「0」と「1」であり、その後の項は常に前の二つの項の合計として計算されます。数式で表すと次のようになります。
- F(n) = F(n-1) + F(n-2)(ただし n ≥ 2)
フィボナッチ数列の初まり
フィボナッチ数列を詳しく見てみると、初めの数値は次の通りです。
- 0
- 1
- 1
- 2
- 3
- 5
- 8
- 13
- 21
- 34
- 55
このように、数列は無限に続くことが特徴です。
加算の基本的なメカニズム
フィボナッチ数列の注目すべき点は、隣接する二つの数値の和が次の数値となることです。例えば、3番目の数「2」は、1番目の「1」と2番目の「1」を足した結果です。また、4番目の数「3」は、2番目の「1」と3番目の「2」を加算することで得られます。この単純な加算のメカニズムが、フィボナッチ数列の魅力と深さを引き立てています。
フィボナッチ数列の実世界への適用
フィボナッチ数列は、数学の領域を超えて、さまざまな現実世界の現象にも見られます。数列が持つ特性や比率は、特に自然科学や経済学の分野で強く利用されています。あなたの身の回りにも、フィボナッチ数列の影響を受けたものが存在するかもしれません。

2. フィボナッチ数の特徴
フィボナッチ数列は、単なる数の列ではなく、非常に多くの興味深い特性を備えています。このセクションでは、フィボナッチ数列についてのユニークな特徴をいくつか掘り下げてみましょう。
隣接項の互いに素性
フィボナッチ数列の際立った特性の一つに、隣接する項同士が互いに素であることがあります。互いに素とは、二つの整数の最大公約数が1であることを意味します。例えば、数5と8を考えてみると、これらは共通の約数を持たないため互いに素です。この性質は、フィボナッチ数列の全ての隣接項に当てはまります。
自然界におけるフィボナッチ数列
フィボナッチ数列は、自然界での多様な現象に現れることでも知られています。特に植物の成長においては、葉の配列や花びらの数、さらにはヒマワリの種の配置にフィボナッチ数がしばしば関与しています。例えば、ヒマワリの種が中心から外側に向かって放射状に並ぶ際、その多くがフィボナッチ数に基づいています。
黄金比との関連
フィボナッチ数列は、黄金比と深い結びつきを持っています。黄金比は約1.618であり、自然界やアートにおいて美しさの象徴とされています。フィボナッチ数列では、隣接する数同士の比率を計算することで、その値が次第に黄金比に近づく様子が見て取れます。このため、フィボナッチ数列はデザインや美術において重要な役割を果たすことが多いのです。
シンプルなルールによる構成
フィボナッチ数列は、単純な規則に基づいて構築されています。具体的には、前の2つの数を加えることで次の数を得る方式です。この数列は以下のように続きます:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
このような簡潔さが、数列を無限に延伸させることを可能にしています。
フィボナッチ比率の活用
フィボナッチ数列から導き出される比率も大いに興味深いです。特に、金融市場でのトレーディングにおいては、フィボナッチ比率がよく利用されています。具体的には、以下のような重要な比率があります。
- 0.236(23.6%): 二つの項を飛ばした次の項で割る
- 0.618(61.8%): 隣接する項で割る
これらの比率は、チャート分析において広く使用され、多くの投資家にとって重要なツールとなっています。
このように、フィボナッチ数列は数学的な美しさだけでなく、自然界や文化に対しても大きな影響を及ぼす、非常に魅力的な数列であることがわかります。
3. フィボナッチ数列の発見者レオナルド・フィボナッチ
フィボナッチの生涯と背景
レオナルド・フィボナッチ(Leonardo Fibonacci)は、1170年頃にイタリアのピサで生まれました。彼は数学者としての才能に恵まれ、中世において商業活動が盛んになっていく時代背景の中で活躍しました。フィボナッチの業績は、商業や数学のみならず、計算方法の発展にも寄与しました。
『算盤の書』の影響
フィボナッチが最も有名な著書『算盤の書』(Liber Abaci)は、1202年に発表されました。この書物では、当時のローマ数字に代わる新たな数の記載法としてインド・アラビア数字を導入し、その利便性を広めました。また、彼はこの書の中で、ウサギの繁殖に関する問題を通じて、フィボナッチ数列を初めて紹介しました。
ウサギの問題
フィボナッチ数列の起源となったのが、ウサギが繁殖する様子に基づく問題でした。彼は、1対のウサギが繁殖する様子を想定し、特定の条件下でどのようにしてウサギの数が増えていくのかを数学的に考えました。このシンプルなモデルが、前の2つの数を足すことで得られる数列を生み出すことになりました。
フィボナッチの業績における革新性
フィボナッチの最大の功績の一つは、当時のヨーロッパにおける数学の分野に革新的な考え方をもたらした点です。彼は、数列だけでなく、数の計算手法や数学的思考を大きく発展させ、後の数学の発展に多大な影響を与えました。彼の発見は、ただの数列にとどまらず、自然界や幾何学にも深く結びついていることを示しています。
フィボナッチにまつわるエピソード
フィボナッチは、彼の業績の中でしばしば「数の魔法」とも表現される独特のパターンを見いだし、多くの人々に感銘を与えました。これにより、彼の名前は数世代にわたり数学の象徴として残り、現代の数学教育にも影響を与えています。
数の普遍性
彼の発見した数列は、単なる数学的なものにとどまらず、自然界やアート、建築などのさまざまな分野にその美や調和を見出す手がかりとなっています。フィボナッチの名は、数列だけでなく、彼の思想や数学的探求をも象徴するものとして広がり続けています。
4. 自然界やアートにおけるフィボナッチ数列
自然界におけるフィボナッチ数列の顕現
フィボナッチ数列は自然の中で数多くの形で見られ、その存在は魅力的です。特に、植物の成長においてこの数列は際立っています。例えば、多くの花の花びらの数は「3」「5」「8」といったフィボナッチ数と一致しています。特にキク科の植物では、13や21といった数字が頻繁に見受けられます。
また、ひまわりの種の配置でもフィボナッチ数列が観察されます。ひまわりは、その種を時計回りと反時計回りに螺旋状に配置し、その数はフィボナッチ数に基づいています。この配置は、植物がどのようにして有限のスペースを最大限に活用しているかを示す良い例です。
動物におけるフィボナッチ数列の役割
フィボナッチ数列は植物だけでなく、動物の体の構造にも見られます。例えば、気管支や肝臓の血管の分岐においてもフィボナッチ数の影響を受けています。これらの分岐は、栄養素と酸素を効率的に運ぶために進化の中で形成されたと考えられています。自然界においては、効率性は生存戦略の一環として非常に重要です。
アートにおけるフィボナッチ数列の影響
フィボナッチ数列はアートの分野でも重要な影響を持っており、数多くのアーティストがその美しい比率に惹かれています。「黄金比」はフィボナッチ数列と無関係ではなく、しばしば美術作品や建築デザインに取り入れられています。例を挙げると、レオナルド・ダ・ヴィンチの名作「モナ・リザ」や、ミロのヴィーナスのプロポーションには、フィボナッチ数列と黄金比が大いに関連しているとされています。
フィボナッチ数列が生む美の魅力
フィボナッチ数列が生み出す形や比率には独特の美しさがあり、それが人々の心に深く響く要因となっています。多くのアーティストやデザイナーは、視覚の調和と心地よさを生み出すために積極的にフィボナッチ数列を取り入れています。このように、フィボナッチ数列は自然界の現象だけでなく、アートの分野においても重要な役割を果たしていることがわかります。

5. FXでのフィボナッチ数列の活用方法
フィボナッチ数列は、FX(外国為替証拠金取引)において非常に重要なテクニカル分析ツールの一つです。特に、フィボナッチリトレースメントを使用することで、市場のトレンドや転換点を予測する手助けとなります。ここでは、フィボナッチ数列の活用方法やその実際の使用例について詳しく見ていきましょう。
フィボナッチリトレースメントとは?
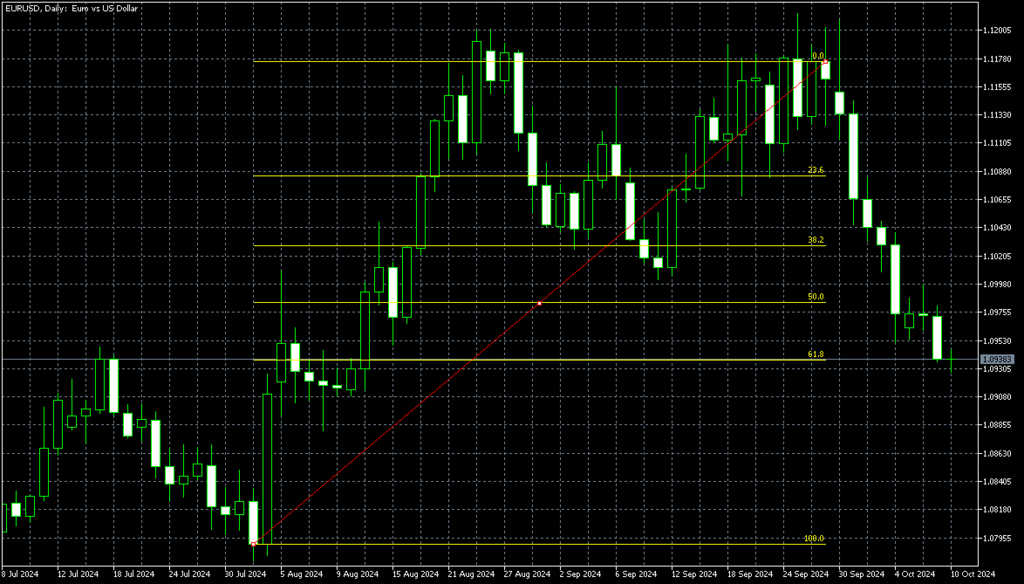
フィボナッチリトレースメントは、トレンドの押し目や戻り目を予測するための手法です。この手法では、高値と安値を基にフィボナッチ比率を用いて、価格がどの程度反発するかを分析します。以下のフィボナッチ比率が特に注目されます。
- 23.6%
- 38.2%
- 50%
- 61.8%
- 100%
これらのレベルをチャート上に引くことで、トレーダーは価格がどのポイントで反転するかの目安を得ることができます。
フィボナッチ数列を使った実際の分析手法
高値と安値を設定する
まず、観察しているチャートの中で、最近の高値と安値を特定します。この2つのポイントを基にフィボナッチリトレースメントを引きます。リトレースメントラインを描く
専用のツールを使用して、特定した高値と安値を基にリトレースメントラインを描画します。これにより、トレーニングや反発が予測される価格レベルが明確になります。シグナルの確認
リトレースメントラインが他のテクニカル指標(移動平均線やサポート・レジスタンスライン)と重なる場合、そのラインはより強力なシグナルとなります。例えば、61.8%のラインが他の確認信号と一致する場合、買いまたは売りのエントリーポイントとして利用できます。
その他のフィボナッチ分析ツール
フィボナッチ数列はリトレースメント以外にも多様な方法で活用できます。以下はその一部です。
フィボナッチファン
高値と安値から放射状にラインを引くことにより、トレンドの変化点を探る手法です。これを用いることで、相場のトレンドラインを把握しやすくなります。フィボナッチアーク
アークを描くことで、価格が変動する範囲や次のサポート・レジスタンスを予測する方法です。アークが価格に対してどのように影響するかを見ることで、トレンドの方向を確認できます。
心理的要因とフィボナッチ
フィボナッチ数列がFX市場で特に有効とされる理由の一つに、トレーダーの心理があります。トレーダーの多くがフィボナッチリトレースメントを活用しているため、自然とこれらの価格レベルが重要視され、相場の反応を引き起こすことが多くなります。このため、フィボナッチを意識したトレーニングを行うことが、期待感や自己の戦略において有利に働くことがあるのです。

まとめ
フィボナッチ数列は単なる数学的なものではなく、自然界やアートの分野にも深く関わり合っている非常に興味深い概念です。その美しい比率や不思議な性質は、私たちの生活に様々な形で影響を与えています。特にFX市場では、フィボナッチ分析が重要なテクニカル指標の一つとなっており、トレーダーにとって有用なツールとなっています。フィボナッチ数列は、数学と自然、そして人間社会の接点を示す素晴らしい存在なのです。
よくある質問
フィボナッチ数列とはどのようなものですか?
フィボナッチ数列は、数列の中で特に有名なものの1つです。最初の2つの数が0と1で始まり、その後の数は前の2つの数の和として計算されます。この簡単な規則により、数列は無限に続いていきます。フィボナッチ数列には多くの興味深い特性があり、自然界や芸術分野でも見られる重要な数列です。
フィボナッチ数列はどのように自然界やアートに活用されているのですか?
フィボナッチ数列は、植物の成長パターンや花びらの数、ひまわりの種の配列など、自然界の多くの現象に深く関わっています。また、建築や絵画、音楽など、アートの分野でも黄金比と関連して重要な役割を果たしています。フィボナッチ数列が生み出す美しい比率は、人々の心を惹きつける魅力的な特徴となっています。
FXでフィボナッチ数列はどのように活用されているのですか?
FXでは、フィボナッチリトレースメントが重要なテクニカル分析ツールの1つとして使用されています。この手法では、過去の高値と安値を基に、価格が反発する可能性のある特定のレベルを見出すことができます。また、フィボナッチファンやフィボナッチアークなどの分析方法も活用されています。トレーダーの心理的要因もフィボナッチ数列の有効性に影響を与えています。
フィボナッチ数列の発見者であるレオナルド・フィボナッチについて教えてください。
レオナルド・フィボナッチは、1170年頃にイタリアのピサで生まれた数学者です。彼が著した『算盤の書』では、インド・アラビア数字の利点を広めるとともに、ウサギの繁殖に関する問題を通してフィボナッチ数列を初めて紹介しました。フィボナッチの業績は、単なる数列にとどまらず、数学の分野全般に革新的な影響を及ぼしました。彼の名は、数学の象徴として世代を超えて受け継がれています。